If F X Changes From Positive to Negative at X C and F is Continuous Then

Point of Inflection - Point of Concavity Change

---

A point of inflection , or point of inflexion, is a point along a curve \(y=f(x)\) at which its concavity changes; it goes from being:

• concave up, \(f''(x)>0\), to concave down, \(f''(x)<0\), or
• concave down, \(f''(x)<0\), to concave up, \(f''(x)>0\).

For the second derivative to change sign it has to go through zero, \(f''(x)=0\).

Consequently we define a point of inflexion as follows:

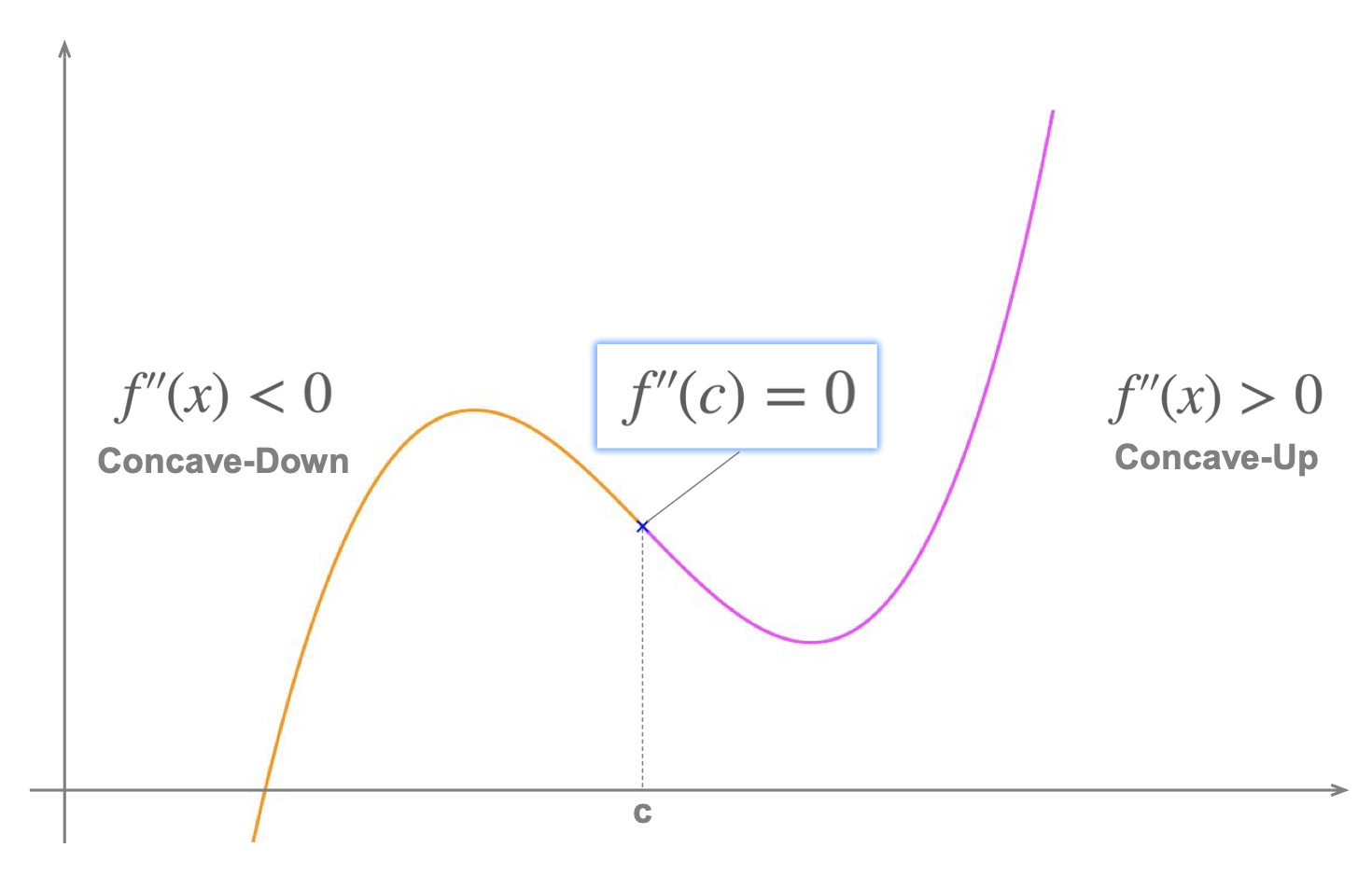
Definition : Point of Inflection

---

Given \(f(x)\), we say that the curve \(y=f(x)\) has a point of inflection at \(x = c\) if and only if:

• \(f''(c)=0\), and
• \(f''(x)\) changes sign on either side of \(x=c\) (positive to negative, or negative to positive).

Careful

: both of these conditions need to be met for there to be a point of inflection at \(x=c\).

In summary a point of inflection is a point across which the curve goes through a concavity change .

---

---

Step by Step Method : Finding a Point of Inflection

---

Given a functions \(f(x)\)

• Step 1: find \(f''(x)\) by successive differentiation.
• Step 2: equate \(f''(x)\) and solve \(f''(x)=0\). If:
  • \(f''(x)=0\) has a solution(s) then move-on to step 3
  • \(f''(x)=0\) has no solution then \(y=f(x)\) doesn't have a point of inflection.
• Step 3: check whether \(f''(x)\) changes sign on either side of \(x=c\) (changes from positive to negative or from negative to positive). If it does then \(y=f(x)\) has a point of inflection at \(x=c\), if it doesn't change sign then it is not a point of inflection.

---

Example 1

Given \(f(x)=x^3-2x^2-8x\) find any point(s) of inflection \(y=f(x)\) may have.

Solution

We follow the 3 steps written above:

• Step 1: find \(f''(x)\). Differentiating with respect to \(x\): \[f'(x)=3x^2-4x - 8\] Differentiating again: \[f''(x) = 6x-4\]

---

• Step 2: Solve \(f''(x)=0\): \[\begin{aligned} & 6x - 4 = 0 \\ & 6x = 4 \\ & x = \frac{4}{6} \\ & x = \frac{2}{3} \end{aligned}\]

---

• Step 3: check whether \(f''(x)\) changes sign.
  • for \(x< \frac{2}{3}\), \(f''(x)<0\)
  • for \(x> \frac{2}{3}\), \(f''(x)>0\)
  Since \(f''\begin{pmatrix}\frac{2}{3}\end{pmatrix}=0\) and \(f''(x)\) changes sign on either side of \(x=\frac{2}{3}\) we can conclude that there is a point of inflection when \(x=\frac{2}{3}\).

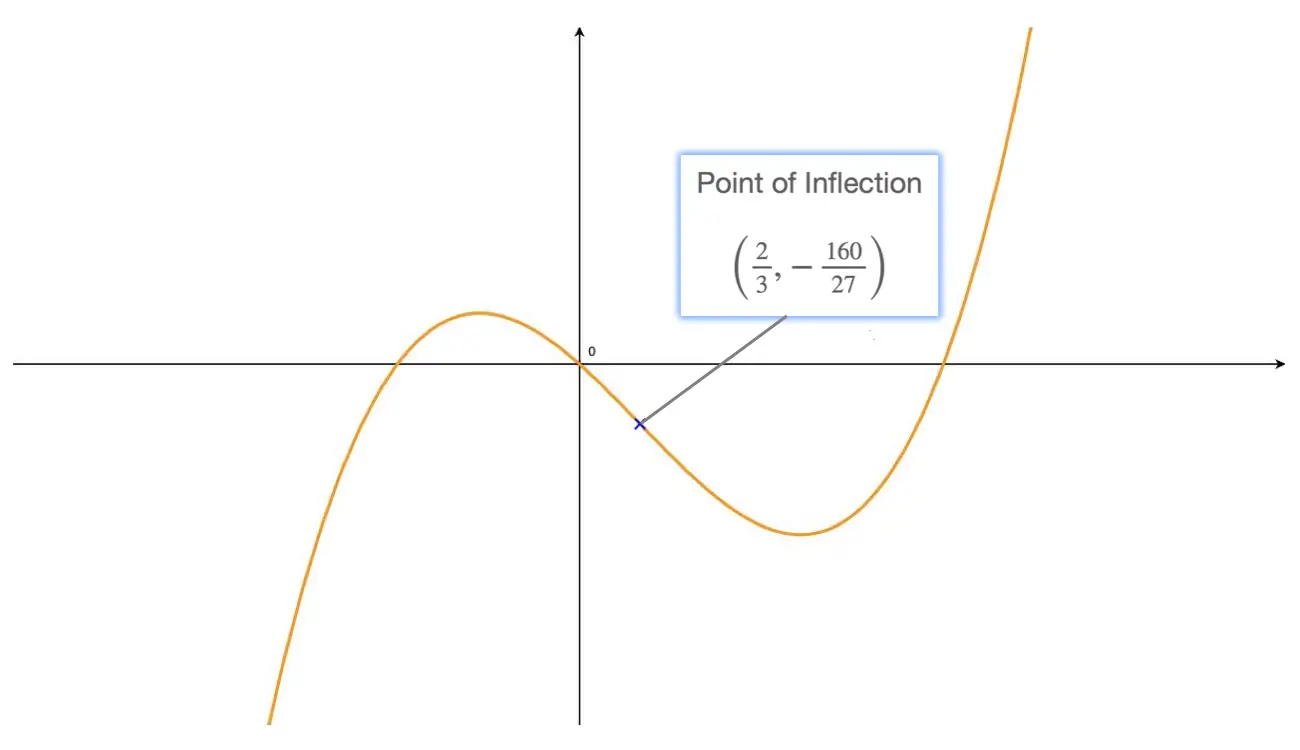Looking at this function's graph, we can see quite clearly that the curve has a point of inflection with coordinates \(\begin{pmatrix} \frac{2}{3},-\frac{160}{27}\end{pmatrix}\); indeed there is a concavity change on either side of this point:

• concave down for \(x<\frac{2}{3}\) (to the left of the point)
• concave up for \(x>\frac{2}{3}\) (to the right of the point)

---

Many curves have more than one point of inflection. The following tutorial is an example.

---

---

Example 2

Given \(f(x) = -\frac{x^4}{2} + 4x^3 + 15x^2 + 2x + 1\), find any points of inflection along the curve \(y=f(x)\).

Solution

We follow the 3 steps written further up:

• Step 1: find \(f''(x)\). Differentiating with respect to \(x\): \[f'(x)=-2x^3 + 12x^2+30x + 2\] Differentiating again: \[f''(x)=-6x^2+24x+30\]

---

• Step 2: Solve \(f''(x)=0\). \[\begin{aligned} & -6x^2+24x+30 = 0 \\ & -6\begin{pmatrix} x^2 - 4x - 5 \end{pmatrix} = 0 \\ & - 6 \begin{pmatrix}x + 1 \end{pmatrix} \begin{pmatrix}x-5 \end{pmatrix} = 0 \end{aligned}\] We can see that \(f''(x) = 0\) has 2 solutions: \[x = -1 \quad \text{and} \quad x = 5\]

---

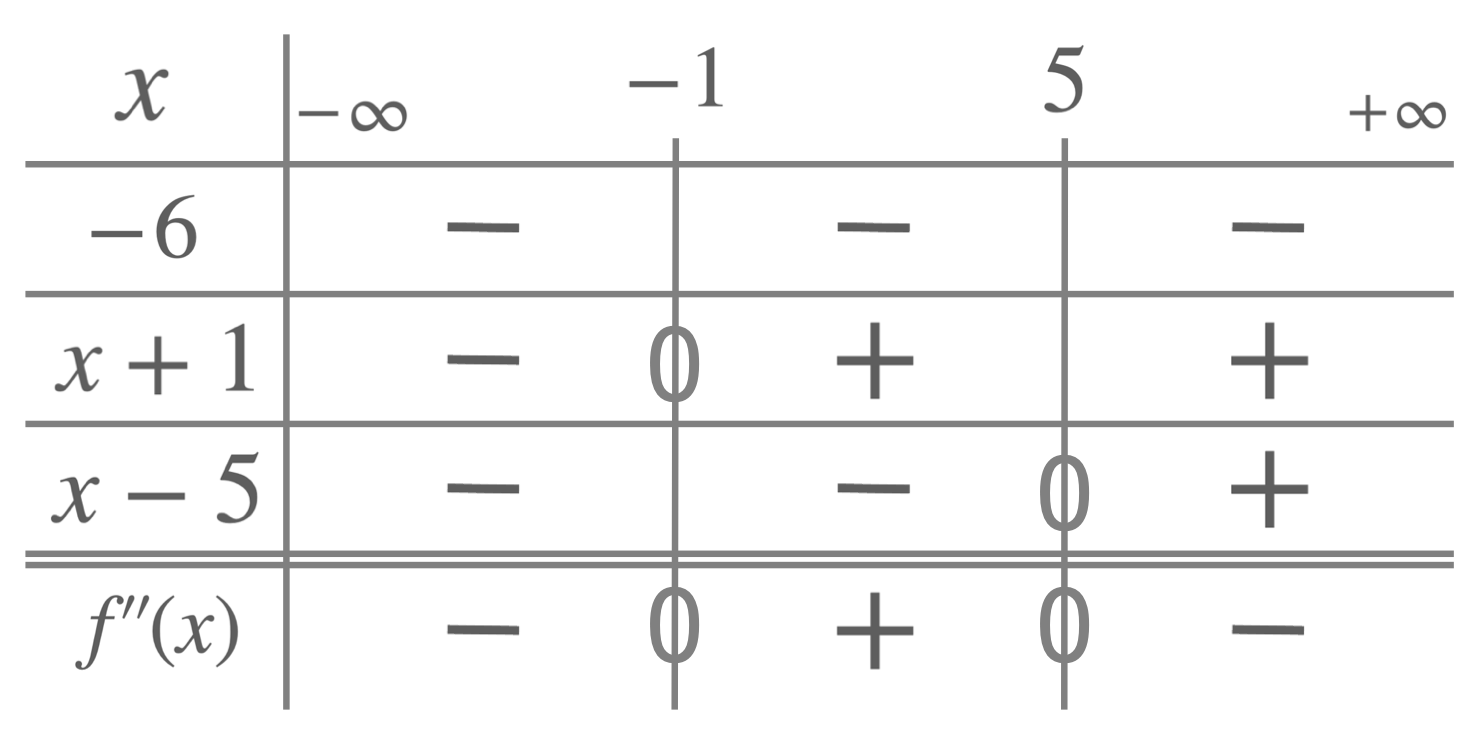
• Step 3: Check that \(f''(x)\) changes sign on either side of these values of \(x\).

  To study the sign of \(f''(x)\), on either side of \(x=-1\) and \(x=5\), we can construct a sign table (as shown here). Using \(f''(x)=- 6 \begin{pmatrix}x + 1 \end{pmatrix} \begin{pmatrix}x-5 \end{pmatrix}\) we study the sign of each of the factors, \(-6\), \(x+1\) and \(x-5\), to then study the overall sign of \(f''(x)\).

  
  On the last row of this sign table, we can see that (as we go from left to right) \(f''(x)\) changes from negative to positive across \(x=-1\) and from positive to negative across \(x=5\). This confirms that the points with \(x\) coordinates \(x=-1\) and \(x=5\) are indeed points of inflection.

---

Finally we can calculate the \(y\)-coordinates of the points of inflection:

at \(x=-1\): \[\begin{aligned} y & = f(-1) \\ & = -\frac{(-1)^4}{2} + 4(-1)^3 + 15(-1)^2 + 2(-1) + 1 \\ & = -\frac{1}{2} - 4 + 15 - 2 + 1 \\ & = -\frac{1}{2} + 10 \\ y & = 9.5 \end{aligned}\] This point of inflection has coordinates \(\begin{pmatrix}-1,9.5\end{pmatrix}\)

at \(x=5\): \[\begin{aligned} y & = f(5) \\ & = -\frac{5^4}{2} + 4\times 5^3 + 15\times 5^2 + 2\times 5 + 1 \\ & = -\frac{625}{2} + 500 + 375 + 10 + 1 \\ & = -312.5 + 886 \\ y & = 573.5 \end{aligned}\] This point of inflection has coordinates \(\begin{pmatrix}5,573.5\end{pmatrix}\)

---

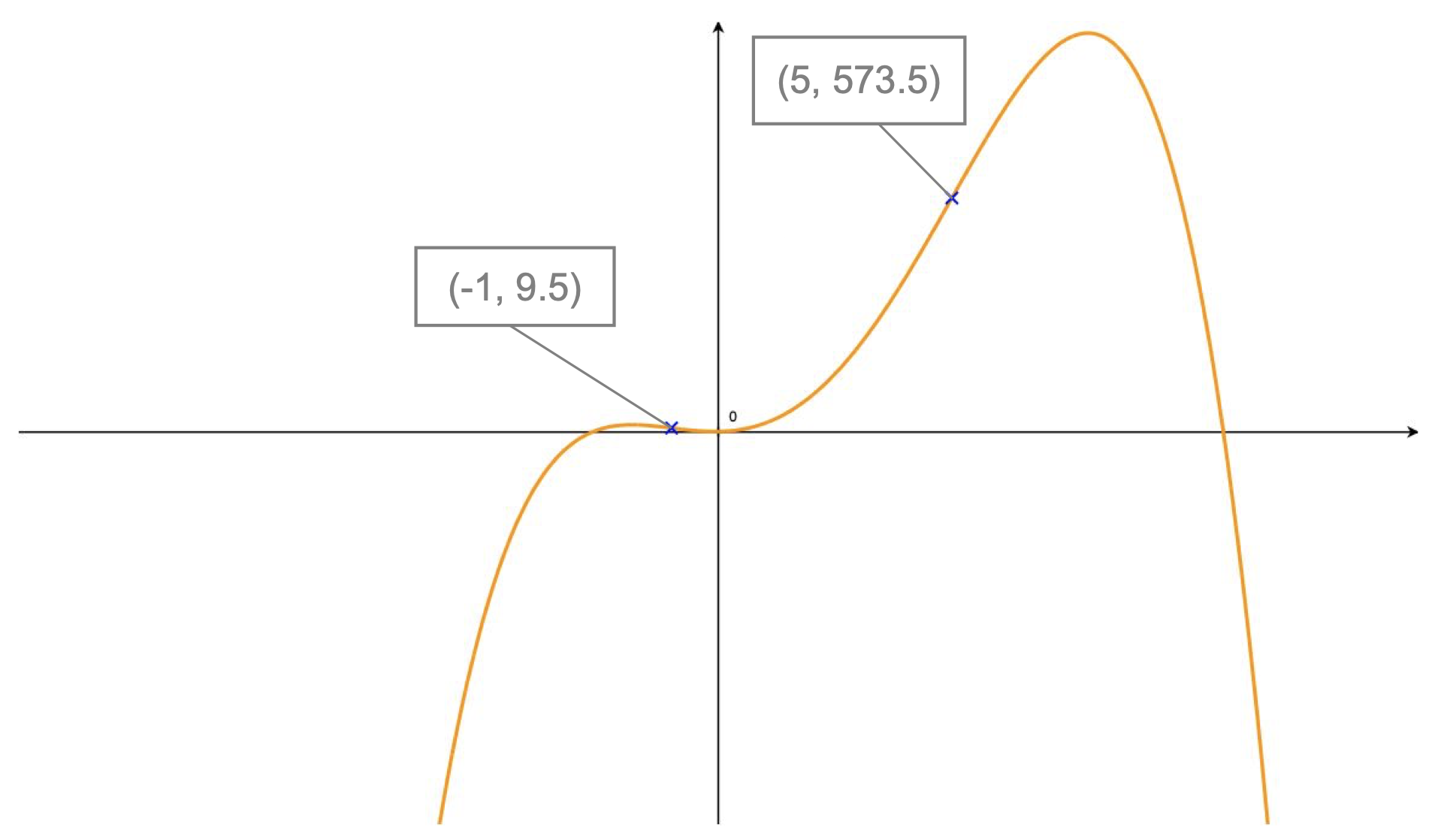
These results are further confirmed by plotting the curve \(y=-\frac{x^4}{2} + 4x^3 + 15x^2 + 2x + 1\). We can see the points of inflection, found above, clearly marking a change in concavity on this curve:

• for \(x < -1 \): the curve is concave-down and \(f''(x)<0\)
• for \(- 1 < x < 5\): the curve is concave-up and \(f''(x)>0\)
• for \(x > 5\): the curve is concave-down and \(f''(x)<0\)

---

Example 3

Given \(f(x) = sin(x)+1.2\), find the points of inflection along the curve \(y=f(x)\) for \(-\frac{3 \pi}{2} \leq x \leq \frac{5 \pi}{2} \).

Solution

Following our 3 step method:

• Step 1: find \(f''(x)\) by successive differentiation \[f'(x) = cos(x)\] differentiating once more: \[f''(x) = -sin(x)\]

---

• Step 2: solve \(f''(x)=0\). Since \f''(x)=-sin(x)\), this results in solving: \[-sin(x)=0, \quad -\frac{3 \pi}{2} \leq x \leq \frac{5 \pi}{2} \] which leads to the 4 solutions: \[x = -\pi, \ 0, \ \pi, \ 2\pi\]

---

• Step 3: check whether \(f''(x)\) changes sign.

  To do this we can study the sign of \(f''(x)\), writing it as \(f''(x)=-1\times sin(x)\) in a sign table, as shown here.

  
  The bottom row of this table clearly shows that \(f''(x)\) changes sign on either side of each of the values \(x = -\pi, \ 0, \ \pi, \ 2\pi\). Each of these values of \(x\) therefore corresponds to a point of inflection.

---

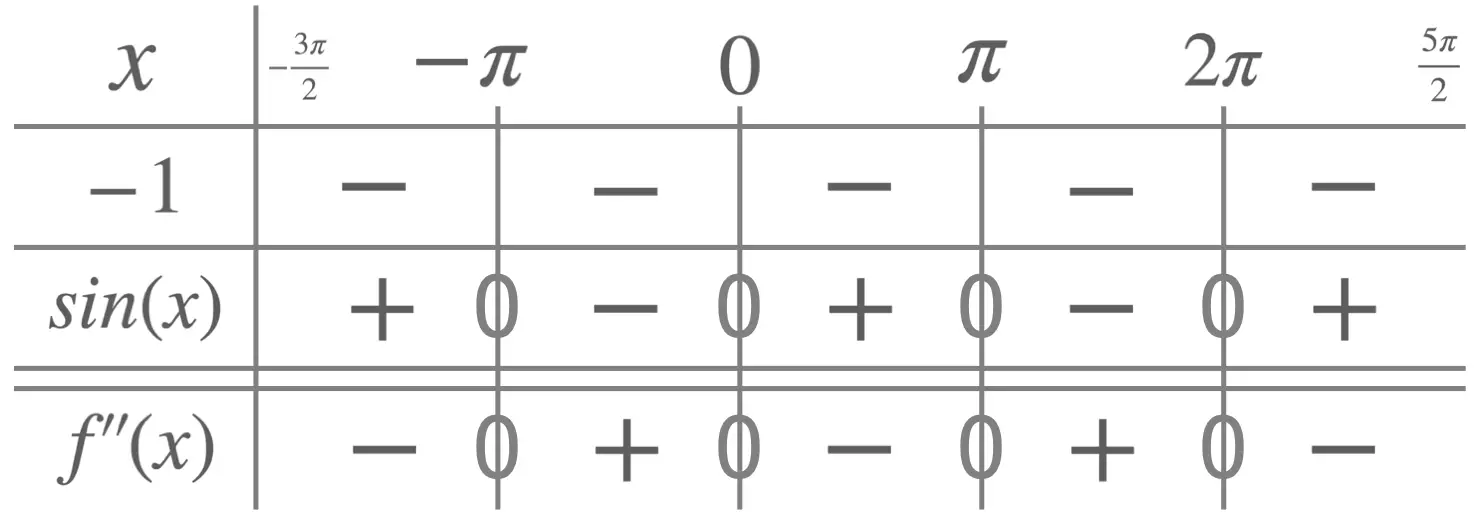
Finally, we can calculate the \(y\)-coordinates of these points of inflection using the equation for \(f(x)\).

Since \(sin\begin{pmatrix}-\pi \end{pmatrix} = sin\begin{pmatrix}0 \end{pmatrix} = sin\begin{pmatrix}\pi \end{pmatrix} = sin\begin{pmatrix}2\pi \end{pmatrix} = 0\)

We quickly find that the points of inflection have coordinates:

\(\begin{pmatrix}-\pi,\ 1.2 \end{pmatrix}\), \(\begin{pmatrix}0,\ 1.2 \end{pmatrix}\), \(\begin{pmatrix}\pi,\ 1.2 \end{pmatrix}\) and \(\begin{pmatrix}2\pi,\ 1.2 \end{pmatrix}\).

hogandamitish77.blogspot.com

Source: https://www.radfordmathematics.com/calculus/Differentiation/point-of-inflection/point-of-inflection.html